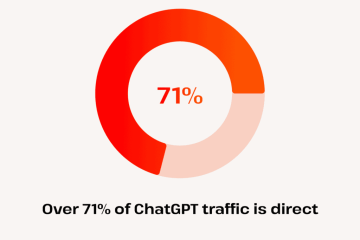
Understanding three: significance in maths and culture
Introduction
The number three is small in size but large in significance. Simple, recognisable and ubiquitous, three appears in mathematics, design, storytelling and daily systems. Its importance lies in providing balance, clarity and a natural rhythm that humans repeatedly use when communicating, organising information or designing structures. This short news-style overview explains why three remains relevant across disciplines and everyday life.
Main body
Mathematical properties
In basic mathematics three is the integer after two and before four. It is the second prime number and the first odd prime. Three forms the basis of many geometric and numerical concepts: a triangle, the simplest polygon, has three sides and three angles, and many counting and combinatorial patterns begin to show structure when grouped into threes. The number three also features in sequences and modular arithmetic as a small modulus that produces simple repeating patterns.
Cultural and practical significance
Beyond pure mathematics, three is embedded in cultural practices and practical systems. Storytelling often uses a three-part structure — setup, confrontation and resolution — to create a clear narrative arc. Rhetoric and memory techniques frequently follow the rule of three, presenting ideas in triplets for emphasis and recall. In everyday systems, traffic lights use three colours to convey stop, caution and go; many user interfaces and design rules recommend grouping items in threes for visual balance; and lists of three are common in journalism and communication because they are easy to process.
Examples in technology and design
Technology also reflects the prevalence of three. Colour models use three primary channels in different contexts: red, green and blue for additive light displays and variations of cyan, magenta and yellow for subtractive printing. Three dimensions define physical space in most contexts, underpinning fields from engineering to virtual modelling. These practical examples show how three provides a compact yet complete framework for many systems.
Conclusion
Three remains a resilient and practical organising principle. For readers, recognising the role of three can improve communication, design choices and understanding of basic mathematical structures. As a concise unit of organisation, three will likely continue to shape storytelling, interfaces and everyday systems where clarity and balance are valued.